PXA-H700 Messungen
 Inhalt:
Inhalt:
- Frequenzgang Übersicht
- Frequenzgang
- Klirrgang
- Dynamik
- Rauschpegel
- Intermodulationsverzerrungen
- Übersprechen
- Frequenzweichen
Frequenzgang Übersicht
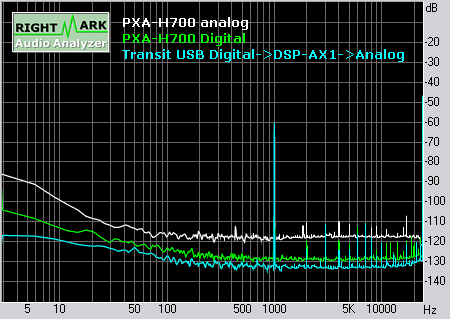
Ich habe mit Rightmark Audio Analyzer und einer M-Audio Transit USB das spektrale Verhalten meines Alpine PXA-H700 untersucht.
Die Messungen wurden jeweils von Front2 des PXA-H700 aufgezeichnet. Dabei waren Equalizer, Frequenzweiche, Media-Expander und BassComp deaktiviert.
Als Ausgang diente der analoge oder digitale Ausgang der M-Audio Transit USB und als Eingang der analoge Line-In der M-Audio Transit USB.
Zum Vergleich habe ich die gleichen Messungen mit der M-Audio Transit USB in Kombination mit meinem Yamaha DSP-AX1 aufgezeichnet. (Transit SPDIF Out -> YAMAHA DSP-AX1 CD-In -> YAMAHA DSP-AX1 Main Pre-Out -> Transit SPDIF Line-In)
Nach den Messungen habe ich Steffens hervorragende Seiten zum Alpine PXA-H700/701 (unter „Technik“) gefunden.
Dort wurde ein Haufen gemessen und beschrieben. Einzig die Phasenfrequenzgänge der Frequenzweichen sind dort nicht beschrieben. Ausserdem glaube ich, dass man die Laufzeitkorrektur besser berechnen, als messen kann.
Messergebnisse:
| Test | PXA-H700 analog |
PXA-H700 Digital |
M-Audio Transit USB SPDIF->DSP-AX1->Line |
| Frequenzgang (40Hz-15kHz) [dB] |
+0.10, -0.13 | +0.07, -0.12 | +0.03, -0.07 |
| Rauschpegel [dB (A)] |
-86.6 | -97.5 | -100.9 |
| Dynamik [dB (A)] |
86.0 | 96.8 | 100.4 |
| Klirrfaktor [%] |
0.0034 | 0.014 | 0.0038 |
| Intermod.- verzerrungen +Rauschen [%] |
0.017 | 0.014 | 0.0066 |
| Übersprechen [dB] |
-83.5 | -88.7 | -78.3 |
Frequenzgang
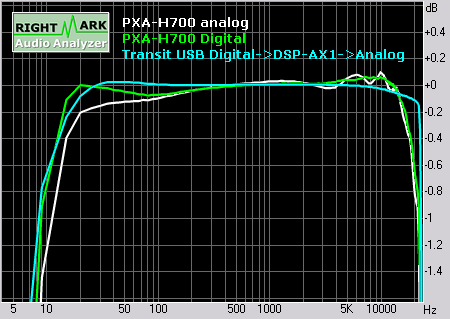
Das gesamte Fenster zeigt einen Bereich von 2dB Höhe.
Die Unterschiede sind (normal) nicht hörbar!
Klirrgang
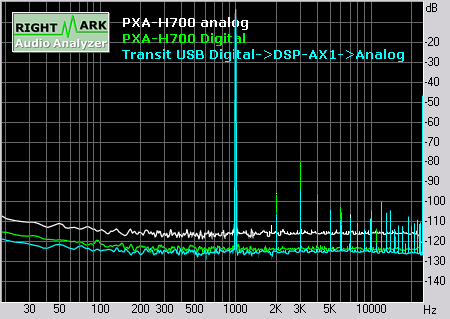
Sollte während der Fahrt nicht wahrnehmbar sein
Dynamikbereich
Rauschpegel
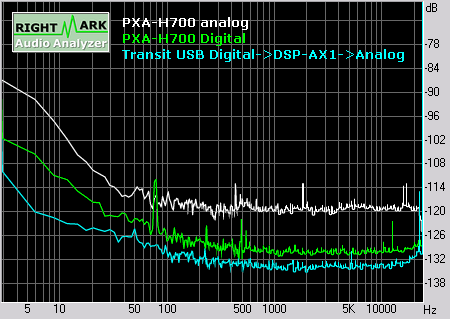
Bei der Aufnahme war die Lautstärkeeinstellung des PXA-H700 auf „22“.
Wenn man sie auf mehr als 28 stellt höre ich das Rauschen im Stand bei laufendem Motor gerade so.
Aber der Fakt alleine das es rauscht, nervt schon!
Intermodulationsverzerrungen
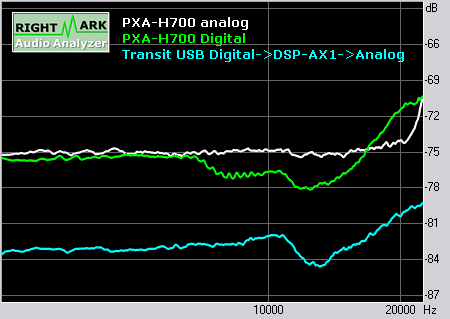
Übersprechen
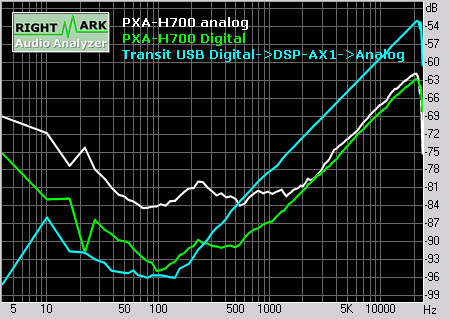
Die Kurven sehen nicht ganz so gut aus. Die 6dB/oct steile Kurve in Richtung hoher Frequenzen in allen Messungen scheint kapazitiver Natur. Das lässt vermuten, dass die von mir verwendeten Kabel (Cinch auf 3.5mm Klinke) der Firma Cordial ab 1kHz zu viel Kapazitive Last für den PXA-H700 darstellen. Bei meinem DSP-AX1 wird es dem Ausgangspuffer bereits ab 200Hz zu viel der Last!
Praktische Auswirkungen hat das Übersprechen jedoch kaum!
Die Übersprechedämpfung im fahrenden Auto mit den Reflektionen an den Scheiben und dem (schlecht gedämmten) Kopf dürfte bei weniger als 6dB liegen.
Also ist alles besser, als es sein müsste 😉
Nebenbei: Ein FM-Tuner hat z.B. weniger als 40dB Stereo-Trennung.
Phasenfrequenzgänge der Frequenzweichen
Ursprünglich stellte ich bei Versuchen, die Laufzeitkorrektur mit dem Laptop zu messen fest, dass der PXA-H700 eine stattliche Verzögerung des Audiosignals von ca. 40ms verursacht. (Das ist auch unangenehm für das Mobiltelefonieren, denn der Anrufer hört oft seine Stimme als Echo!) Also ging ich davon aus, dass Alpine FIR-Filter verwendet, um alles in einem Rutsch zu berechnen (LZK, EQ, XO). Damit wäre es möglich, mit linearer Phase zu arbeiten.
Beim Suchen der richtigen Filtersteilheit und Trennfrequenz der Frequenzweichen fiel mir arg auf, dass bei 12dB/oktave um die Grenzfrequenz herum nur Matsch zu hören ist 😕 . Nach instinktivem Drehen der Phase der Tiefmitteltöner war der Matsch weg! 😯
Durch Zuschalten meines Hirns erkannte ich schnell, dass man mindestens 100ms Verzögerung braucht, um ein Linearphasiges FIR-Filter für 20Hz hinzubekommen. (1/20Hz = 50ms, plus 50ms für Spiegelkoeffizienten (=lineare Phase) plus LZK >=100ms!). Der PXA-H700 ist also nicht phasenlinear. Das wollte ich genauer wissen!
Zum Messen der Phasenfrequenzgänge habe ich ARTA benutzt.
Dabei habe ich festgestellt, dass die benutzten digitalen Filter analoge Vorbilder haben.
Die Filter in den Frequenzweichen des PXA-H700 entsprechen:
| Steilheit | Analoges Filter(-vorbild) | Phasendifferenz bei Grenzfrequenz |
| 6dB | Butterworth 1ter Ordnung | 90° (HP +45°, TP -45°) |
| 12dB | Butterworth 2ter Ordnung | 180° (HP +90°, TP -90°) |
| 18dB | Bessel 3ter Ordnung | 270° (HP +135°, TP -135°) |
| 24dB | Linkwitz-Riley 4ter Ordnung | 360° (HP +180°, TP -180°) |
| 30dB | Bessel 5ter Ordnung | 450° (HP +225°, TP -225°) |
Wenn man die Lautsprecher oberhalb deren Resonanzfrequenz betreibt (Was bei meinem Subwoofer z.B. nicht der Fall ist), sind IMHO nur bei 24dB/oktave mit allen LSP in Phase und 12dB/oktave mit verdrehtem Tiefmitteltöner vernünftige Klangbilder zu erzielen.
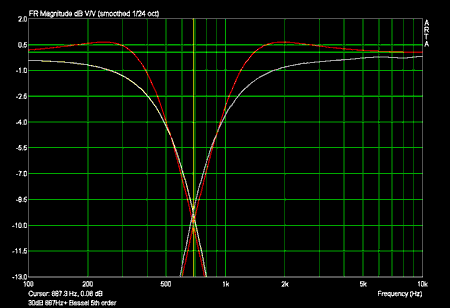
Bei eingestellten 630Hz ist die tatsächliche Übernahmefrequenz ca 687Hz!
Phasenfrequenzgänge (gesamt):
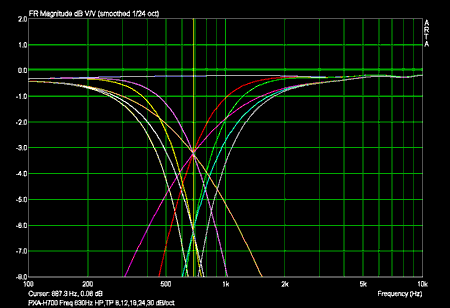
Hinweis: Der Schnittpunkt der 30dB/oktave Filter liegt bei -9dB.
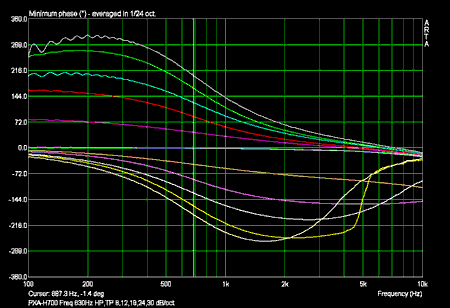
Die Phasen der Tiefpässe in hohen Frequenzen sind durch die kleine Amplitude falsch!
Die Phasen der Hochpässe in tiefen Frequenzen sind durch die kleine Amplitude falsch!
Phasenfrequenzgänge 6dB/oktave mit Sollfrequenzgang eines Butterworth Filters 1ter Ordnung (in rot):
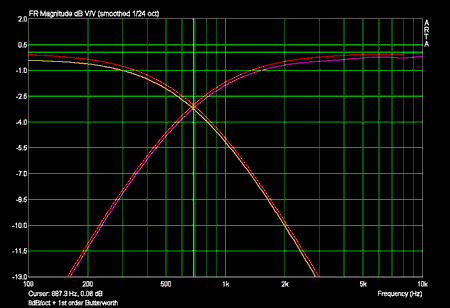
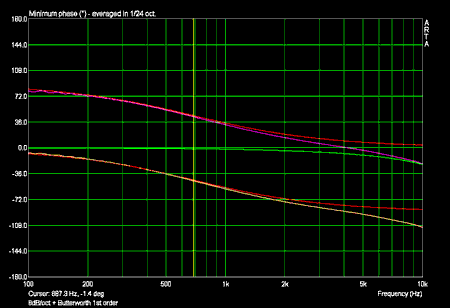
Die Phase des Tiefpasses in hohen Frequenzen und die Phase des Hochpasses in tiefen Frequenzen sind durch die kleine Amplitude verfälscht!
Phasenfrequenzgänge 12dB/oktave mit Sollfrequenzgang eines Butterworth Filters 2ter Ordnung (in rot):
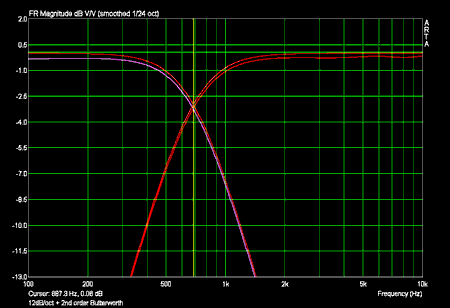
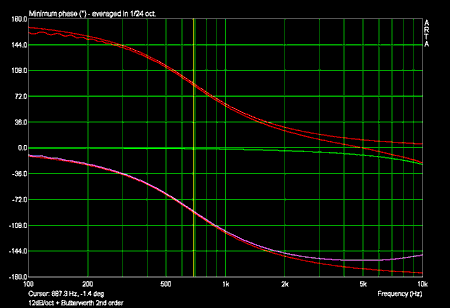
Die Phase des Tiefpasses in hohen Frequenzen und die Phase des Hochpasses in tiefen Frequenzen sind durch die kleine Amplitude verfälscht!
Phasenfrequenzgänge 18dB/oktave mit Sollfrequenzgang eines Bessel Filters 3ter Ordnung (in rot):
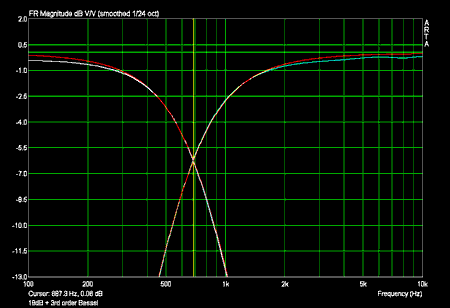
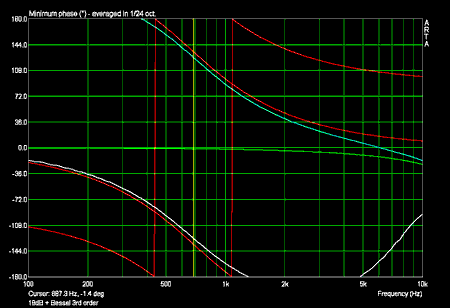
Die Phase des Tiefpasses in hohen Frequenzen und die Phase des Hochpasses in tiefen Frequenzen sind durch die kleine Amplitude verfälscht!
Phasenfrequenzgänge 24dB/oktave mit Sollfrequenzgang eines Linkwitz-Riley Filters 4ter Ordnung (in rot):
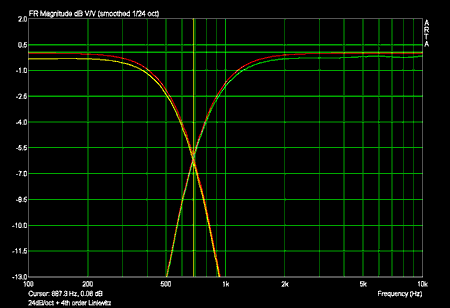
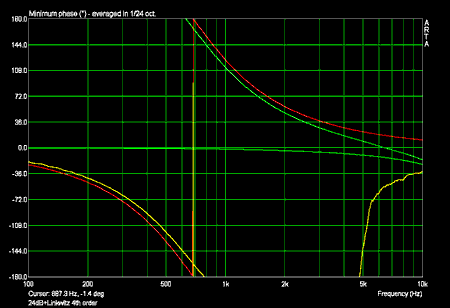
Die Phase des Tiefpasses in hohen Frequenzen und die Phase des Hochpasses in tiefen Frequenzen sind durch die kleine Amplitude verfälscht!